/ Home / Research / Superconductivity

High Temperature Superconductivity

The high transition temperature (high-Tc) cuprate superconductors have been a perennial area of interest for our lab. These materials have held a prominent position in the field of condensed matter physics since they were discovered twenty years ago, yet many mysteries still remain regarding the fundamental mechanism behind the superconductivity they exhibit. Open questions include the pseudogap state, the energy scales of condensate formation, the relationship with magnetic order, and the role of inhomogeneity, among others [Rev. Mod. Phys. 77, 721 (2005)]. Our recent work is focused both on cuprate high-Tc superconductors (eg.: YBa2Cu3Oy and La2-xSrxCuO4) and also newly discovered FeAs- and FeP-based high-Tc materials [CondMat-arXiv:0808.3748]. The broadband magneto-spectroscopy instrumentation in our infrared laboratory at UCSD places us in a unique position to address these questions.  Measurements in magnetic field are particularly useful because electronic properties can be directly tuned without introducing obscuring effects.

 

Recent research highlight: Interlayer coherence and superconducting condensate in the c-axis infrared response of optimally doped Ba(Fe1-xCox)2As2 [S. J. Moon et al., Phys. Rev. Lett. 110, 097003 (2013)]

Superconductivity at genuinely high-transition temperature Tc exceeding 40-50 K is only observed in layered materials such as cuprates and iron-based compounds. Unraveling the role of electronic anisotropy imposed by the layered crystal structure constitutes an important step toward the understanding of the high-Tc phenomenon. We succeeded in probing the intrinsic interlayer response by performing infrared experiments on the crystals with cleaved ac surface for the first time. Our experiments identify the coexistence of the suppression of the electronic spectral weight and the development of a coherent Drude-like response in the normal-state. The formation of the interlayer condensate is clearly observed in the superconducting state and appears to be linked to coherent contribution to the normal-state conductivity.

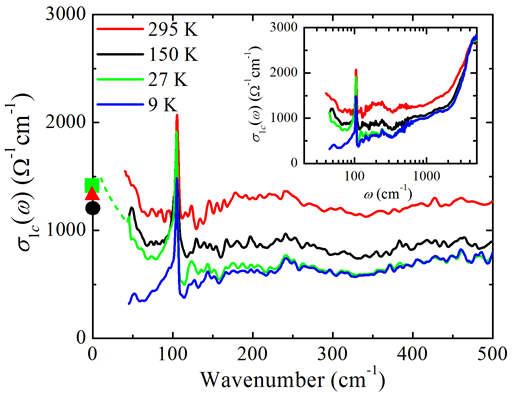
Caption: Real part of the c-axis optical conductivity of optimally doped Ba(Fe_0.926Co_0.074)₂As₂. The solid circle, triangle, and rectangle denote the dc conductivity values at 295, 150, and 27 K, respectively. As T decreases, s_1c(ω) in the far-infrared frequency region becomes depressed and the suppressed spectral weight is most likely not recovered up to 4000 cm^-1, as shown in the inset. The dashed lines represent the extrapolated s_1c(ω) at T=27 K using the Hagen-Rubens analysis of R_c(ω). In the superconducting state, s_1c(ω) exhibits substantial depression below about 250 cm^-1 with spectral weight transfer into the superconducting condensate d peak at ω=0.

 

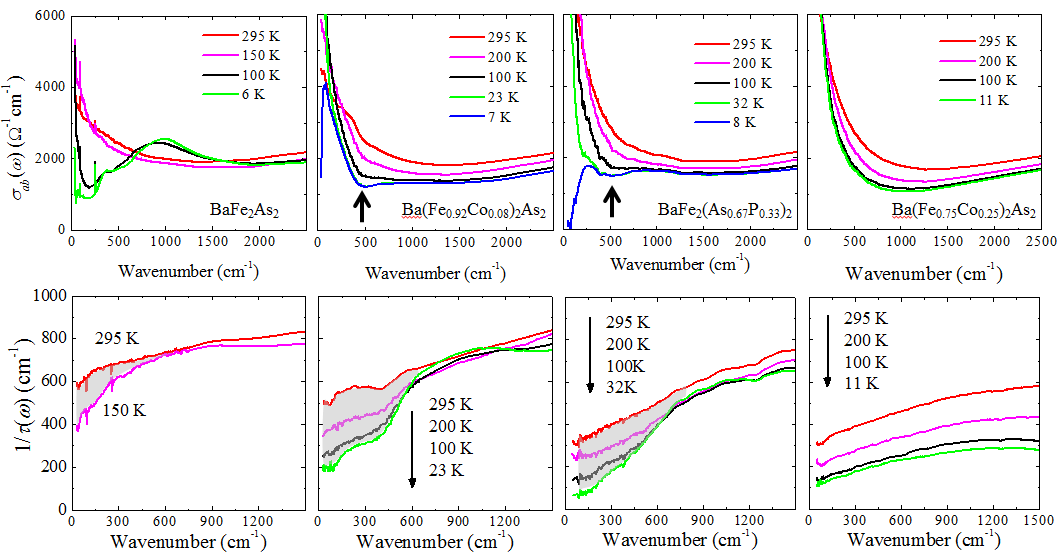
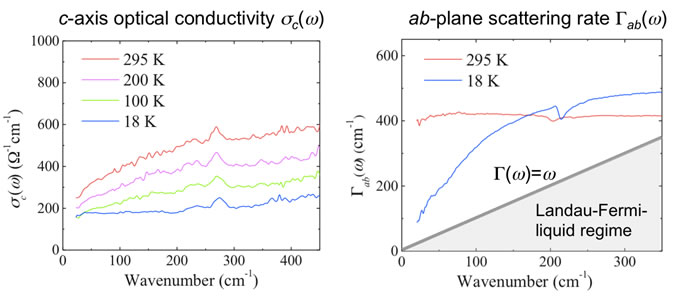
Recent research highlight: Infrared probe of the pseudogap in high-Tc BaFe₂As₂ superconductors [S. J. Moon et al., Phys. Rev. Lett. 109, 027006 (2012)]

This study focuses on the pseudogap feature in the prototypical Fe-based superconductors: BaFe₂As₂ system. The nature of pseudogap phase and its relation to high-Tc superconductivity remains a significant problem in condensed matter physics. Our infrared experiments have identified hallmarks of the pseudogap state in BaFe₂As₂ system that mirror spectroscopic manifestations of the pseudogap in the cuprates. The pseudogap formation is manifested by the weak absorption feature followed by featureless mid-infrared conductivity in the conductivity and by the suppression in the scattering rate below a certain frequency in the parent and optimally doped compounds. Such spectral features are absent in overdoped crystal. The evolution of the optical spectra with doping and temperature suggests that the pseudogap in the BaFe₂As₂ system can be related to spin/orbital fluctuations.

Caption: (a)-(d) Real part of the optical conductivity s_ab(ω) of BaFe₂As₂, Ba(Fe_0.926Co_0.074)₂As₂, BaFe₂(As_0.67P_0.33)₂, Ba(Fe_0.75Co_0.25)₂As₂ from left to right. The parent BaFe2As2 show antiferromagnetic transition at T_N=135 K. The conductivity spectra show drastic changes across T_N, which are attributed to the spin-density-wave gap formation. The arrows in (b) and (c) denote the frequency position above which s_ab(ω) shows slight increase due to the pseudogap formation. (e)-(h) Scattering rate. The gray area highlights the suppression in the scattering rate due to the pseudogap formation. The threshold frequency correlates with the spin-density-wave gap in s_ab(ω) of BaFe₂As₂.

 

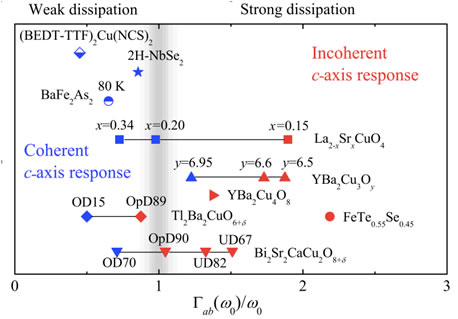
Recent research highlight: Incoherent c-axis electronic response of FeTe0.55Se0.45 superconductor [S. J. Moon et al., Phys. Rev. Lett. 106, 217001 (2011).]

The iron-based superconductors have layered crystal structure that results in a strong electronic anisotropy. Whereas the ab-plane electronic response has been extensively investigated, much less is known about the c-axis properties. In this study, we investigated interlayer c-axis infrared response of FeTe_0.55Se_0.45superconductor. We find that the c-axis electronic response of FeTe_0.55Se_0.45 is incoherent and bears close similarities with the pseudogap phenomena in the underdoped cuprates.

Caption: The c-axis optical conductivity s_c(ω) does not exhibit Drude response. As temperature decreases, the featureless s_c(ω) is further decreased. The spectral weight removed from low frequencies are transferred to higher energies (top left). The incoherent c-axis response is found to be associated with the strong dissipation in the ab-plane response. Note that the magnitude of the ab-plane scattering rate Γ_ab(ω) is larger than the frequency (top right). We find that the interdependence between the degree of c-axis coherence and the ab-plane dissipation holds true for various correlated materials (bottom). The gray bar denotes the region close to Γ_ab(ω)~ω. The left and right sides of this region represents the weak and strong dissipation regimes, respectively. The majority of the materials with strong (weak) ab-plane dissipation exhibit incoherent c-axis response plotted with red (blue) symbols.

 

Recent research highlight: Magnetic field-induced two-dimensional superconductivity and the breakdown of the universal Josephson relation [Schafgans, et al., Phys. Rev. Lett. 104, 157002 (2010); Schafgans, et al., Phys. Rev. B 82, 100505(R) (2010).]

These studies focus on the behavior of the Josephson plasma resonance (JPR) in a number of La-based cuprate superconductors as a function of temperature and applied magnetic field.  The Josephson plasma resonance is formed by a collective oscillation (plasma resonance) of superconducting Cooper pairs between the CuO2 planes (c-axis). Because electronic transport along the c-axis involves quantum tunneling and is not facilitated by orbital overlap as in metals, the conduction of Cooper pairs along the c-axis is described by Josephson physics (hence, Josephson plasma resonance). Since Josephson coupling mediates the c-axis superfluid density, the JPR is sensitive to the phase relationship of the local superconducting order parameter between neighboring CuO2 planes. Any process which, on average, produces a phase difference between layers and suppresses the superfluid density should be evident in the JPR.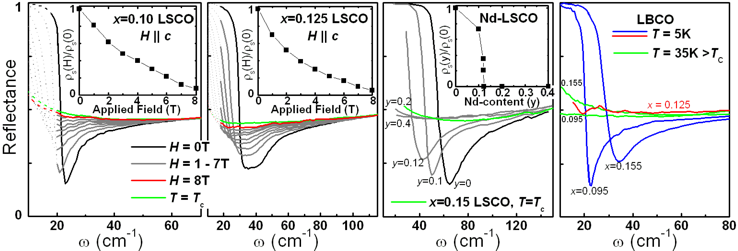

Figure 1: Upon the application of an external magnetic field oriented along the crystallographic c-axis (H || c), we find that the JPR is completely suppressed with a moderate magnetic field (Figure 1, panels a and b) while the in-plane superfluid remains mostly unaffected (See Schafgans, PRL ‘10). This is in stark contrast to the expected behavior of the JPR in light of the universal Josephson relation [Homes, et al. Nature 430, 539 (2004)] yet is remarkably similar to the peculiar doping-induced suppression of the JPR in other La-based cuprate superconductors (Figure 1, panels c and d) (See Schafgans, PRB Rapid ’10). We conclude that the suppression of the JPR is due to the onset of in-plane, static magnetic order that enforces a strict phase relationship of the superconducting order parameter, effectively eliminating Josephson coupling of the CuO2 planes up to the 4th nearest neighbor.

[1] S. J. Moon, Y. S. Lee, A. A. Schafgans, A. V. Chubukov, S. Kasahara, T. Shibauchi, T. Terashima, Y. Matsuda, M. A. Tanatar, R. Prozorov, A. Thaler, P. C. Canfield, S. L. Bud'ko, A. S. Sefat, D. Mandrus, K. Segawa, Y. Ando, and D. N. Basov Phys. Rev. B 90, 014503 (2014).